This is a memo summarizing numeral system problems that frequently appear in the Ruby Certification Exam.

Table of Decimal, Binary, Hexadecimal, and Octal Numbers

Decimal	Binary	Hexadecimal	Octal
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	8	10
9	1001	9	11
10	1010	A	12
11	1011	B	13
12	1100	C	14
13	1101	D	15
14	1110	E	16
15	1111	F	17
16	10000	10	20

Frequently Used Methods

hex Method

The hex method interprets a string as a hexadecimal representation and converts it to an integer. The string may or may not start with “0x”. It extracts and converts the portion of the string that can be interpreted as hexadecimal. If no such portion exists, it returns 0.

to_i Method

The to_i method interprets a string as a decimal representation and converts it to an integer. It extracts and converts the portion of the string that can be interpreted as decimal. If no such portion exists, it returns 0.

By default, it assumes decimal. If an argument is specified, it can convert representations other than decimal (from base 2 to 36). If the base is set to 0, it determines the base from the prefix.

Prefixes include 0b (binary), 0 (octal), 0o (octal), 0d (decimal), and 0x (hexadecimal).

The base is an integer that specifies the numeral system. It can be 0 or an integer from 2 to 36. If set to 0, it defaults to decimal. If a negative value is specified, it raises an ArgumentError exception.

oct Method

The oct method interprets a string as an octal representation and converts it to an integer. The string may or may not start with “0” or “0o”. It extracts and converts the portion of the string that can be interpreted as octal. If no such portion exists, it returns 0.

How to Calculate Numeral Systems

This is a personal memo.

What is Decimal?

We often skip over this because we use it every day, but it’s essential to understand.

Let’s take 1504 as an example.

• 1 represents the “number of thousands.”
• 5 represents the “number of hundreds.”
• 0 represents the “number of tens.”
• 4 represents the “number of ones.”

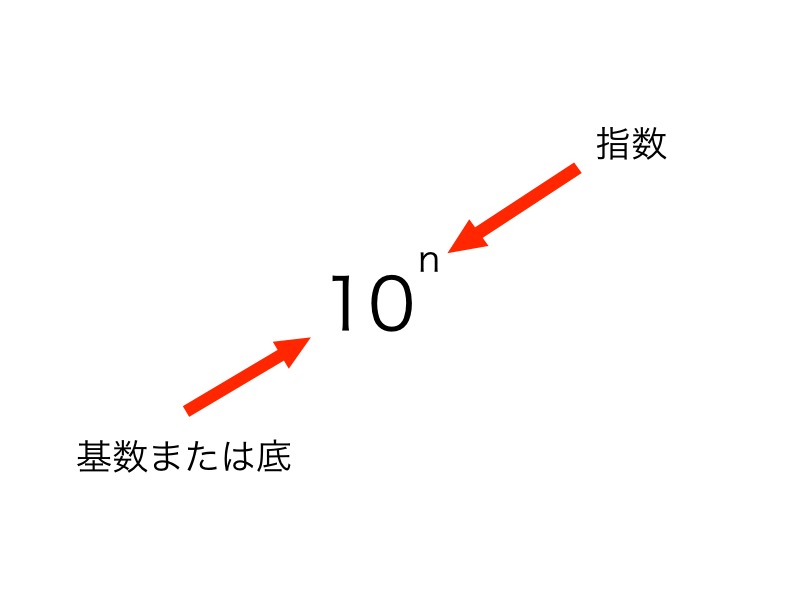
Here’s a diagram:

This “10” is called the base or radix of the decimal system. The numbers in the superscript are called exponents.

What is Binary?

• Only two digits: 0 and 1.
• From right to left, it represents the units place, twos place, fours place, eights place, and so on. Essentially, the nth digit represents 2^(n-1).

When counting in binary, it goes 0, 1, then 10 (not 2), followed by 11, 100, 101, and so on.

Let’s take the binary number 1100 as an example.

• 1 represents the “number of eights” ← 4th digit, so 2³ = 8
• 1 represents the “number of fours” ← 3rd digit, so 2² = 4
• 0 represents the “number of twos” ← 2nd digit, so 2¹ = 2
• 0 represents the “number of ones” ← 1st digit, so 2⁰ = 1

Thus, converting binary 1100 to decimal looks like this:

1 × 2³ + 1 × 2² + 0 × 2¹ + 0 × 2⁰ = 1 × 8 + 1 × 4 + 0 × 2 + 0 × 1
                                  = 8 + 4 + 0 + 0
                                  = 12

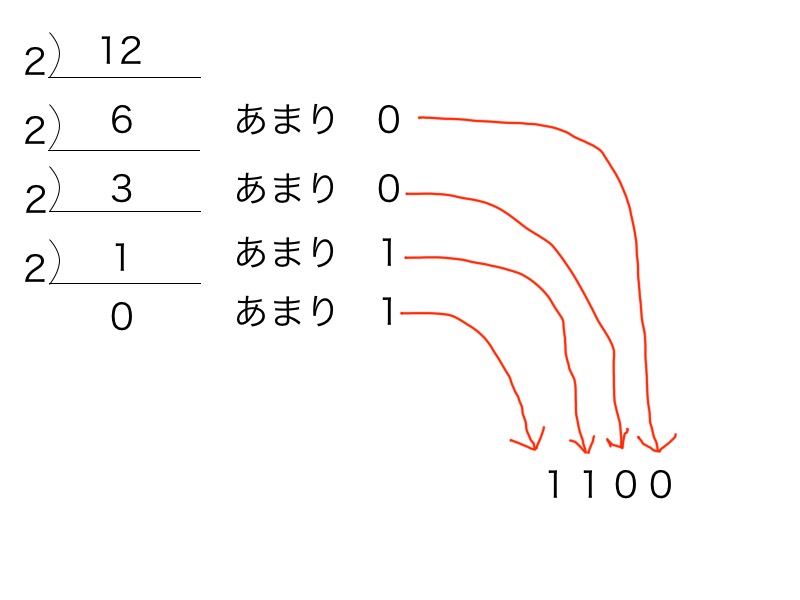
To convert decimal 12 to binary, it looks like this:

What is Octal?

Octal is a numeral system that uses eight digits, from “0” to “7”.

Let’s take the octal number 371 as an example.

• 3 represents the “number of sixty-fours” ← 3rd digit, so 8² = 64
• 7 represents the “number of eights” ← 2nd digit, so 8¹ = 8
• 1 represents the “number of ones” ← 1st digit, so 8⁰ = 1

Thus, converting octal 371 to decimal looks like this:

3 × 8² + 7 × 8¹ + 1 × 8⁰ = 3 × 64 + 7 × 8 + 1 × 1
                          = 192 + 56 + 1
                          = 249

What is Hexadecimal?

Hexadecimal is a numeral system that uses 16 symbols: the digits 0 to 9 and the letters A to F.

Let’s take the hexadecimal number 3F7B as an example.

• 3 represents the “number of four-thousand-ninety-sixes” ← 4th digit, so 16³ = 4096
• F represents the “number of two-hundred-fifty-sixes” ← 3rd digit, so 16² = 256
• 7 represents the “number of sixteens” ← 2nd digit, so 16¹ = 16
• B represents the “number of ones” ← 1st digit, so 16⁰ = 1

Thus, converting hexadecimal 3F7B to decimal looks like this:

3 × 16³ + F(15) × 16² + 7 × 16¹ + B(11) × 16⁰ = 3 × 4096 + 15 × 256 + 7 × 16 + 11 × 1
                                              = 12288 + 3840 + 112 + 11
                                              = 16251

For those from a humanities background, this can be a bit challenging. The following book was used as a reference. It’s worth buying.

• Create Individual Files from CSV Using Ruby
• Use eval to clear up a lot of conditionals.
• What is ruby's initialize method?